DT5 | Deriving Trigonometry - Double Angle Formulae

In last week's section of Deriving Trigonometry, we established the following identities:

In this section, we are going to build upon these identities to form the double angle identities.

To achieve that, we can simply do this:

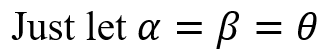
We would then obtain the following for sine:

And cosine:

Something about cosine looks familiar. Remember this identity?

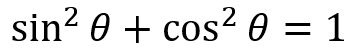
Well we could substitute this into the identity for cosine, and get these following ones:

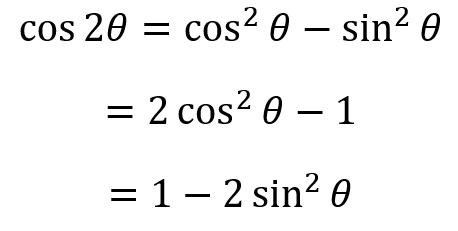
This is why the cosine double angle formula always shows up in these 3 forms. All 3 are interchangeable, and it is good to acknowledge all of them.

And lastly, we have the tangent double angle formula:

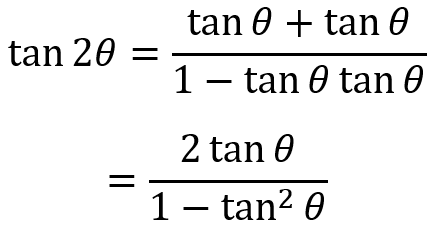
In closing, we have the following double angle formulae:

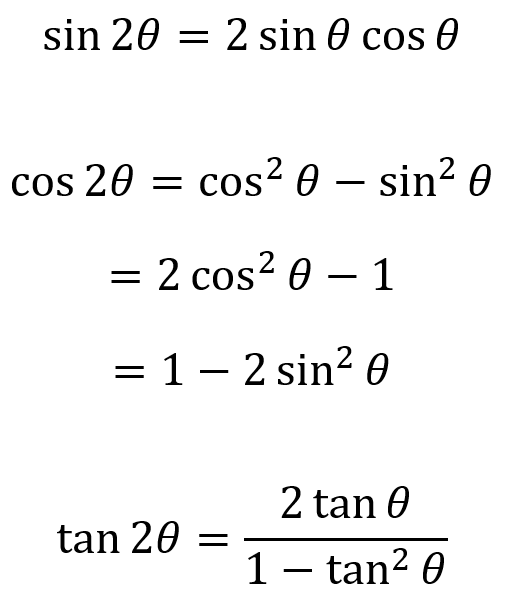
Next week, we will extend the formula list to include triple angles.

Give yourself a moment to think about how you can achieve triple angles with the sum and difference formulae.

That's all for Messy Workings! Thank you for reading :)