DT4 | Deriving Trigonometry - Sum and Difference Formulae

Sometimes we know the ratios of two angles separately, but not the sum of them. The question if it's possible to have an expression that easily shows what the ratio of the sum of the angles are.

Let's set out to answer this question.

Picture two right angled triangles stacked on top of each other, within a bounding rectangle:

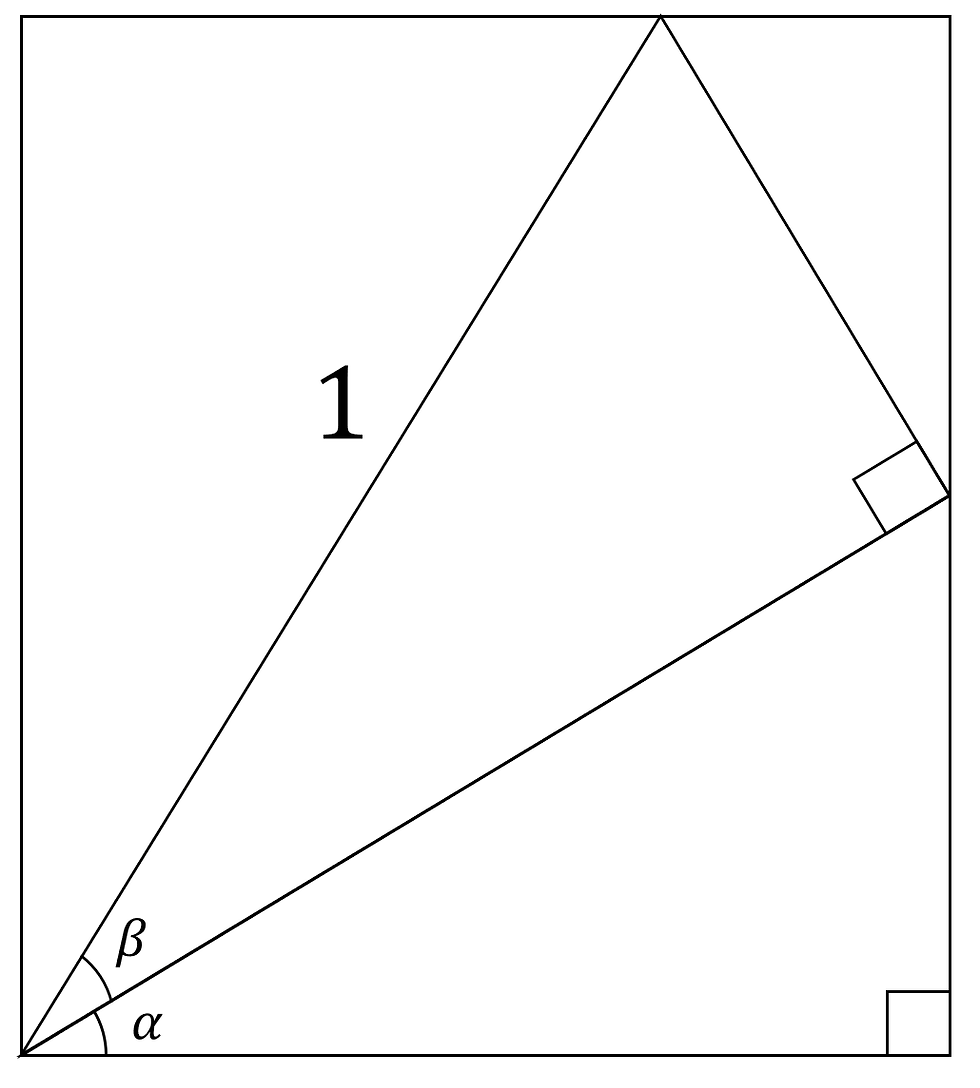
The bottom triangle has an acute angle of α and the top triangle has an acute angle of β. The hypotenuse of the top triangle is 1 unit in length.

Given this information, we can use our knowledge from Deriving Trigonometry 2 (DT2) to label the lengths of the triangles, treating the angle β as subtended from the unit circle, part of the triangle with hypotenuse 1.

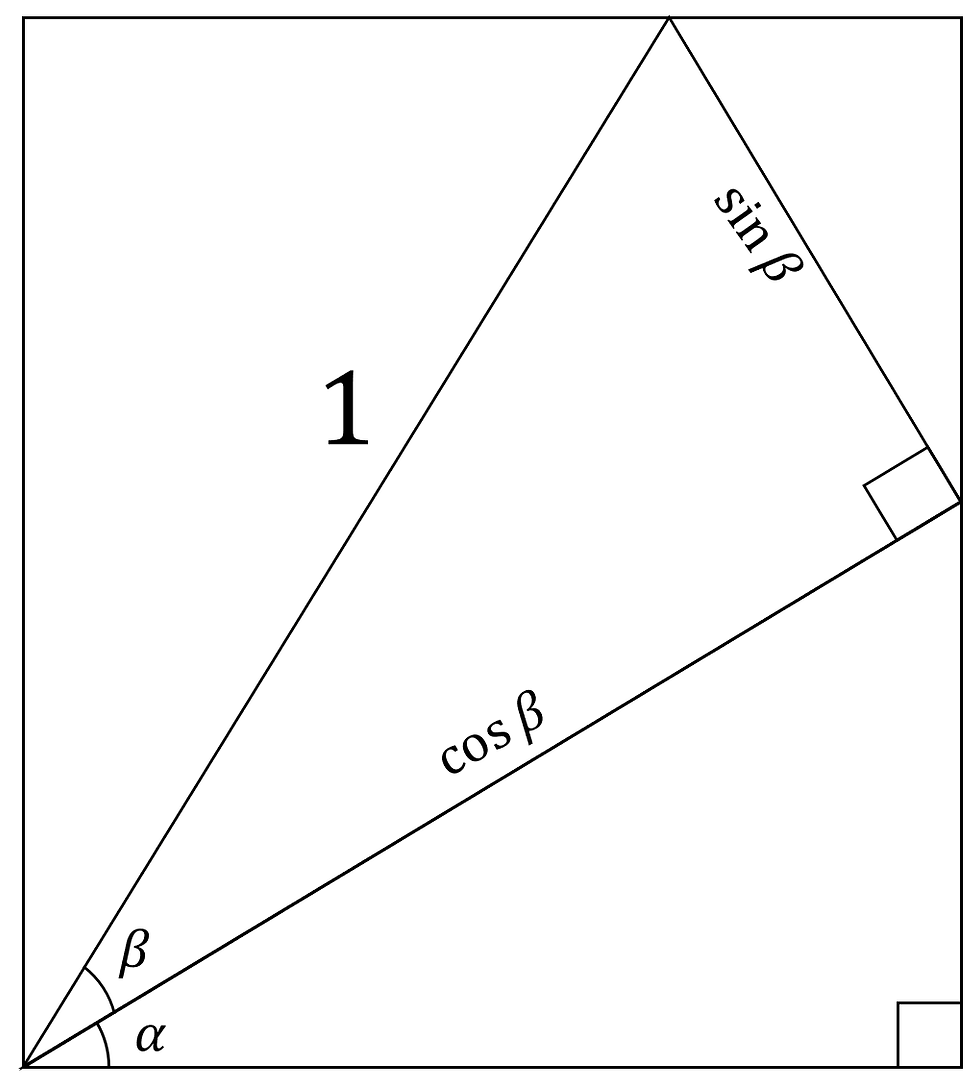
So it is straightforward to label the opposite side as sinβ and the adjacent side as cosβ.

Moving along to the triangle with α, we can label the sides as such:

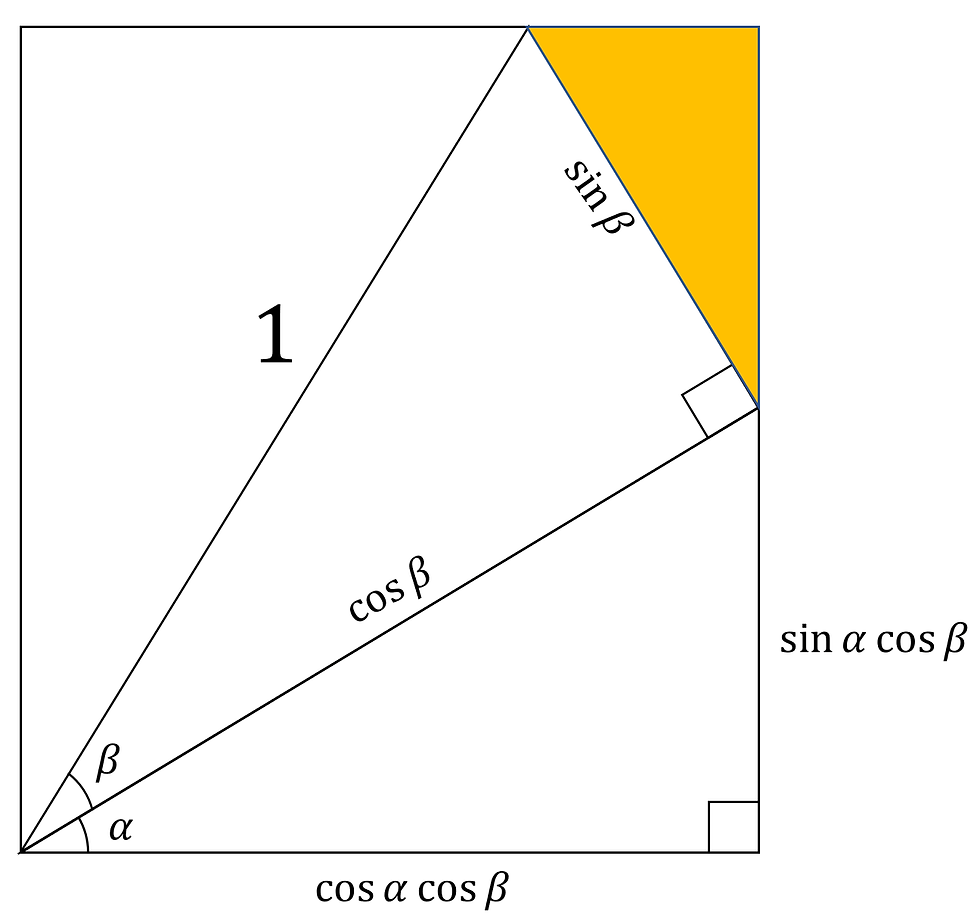
Notice now the triangle shaded in orange.

We can figure out the angles it contains by doing this:

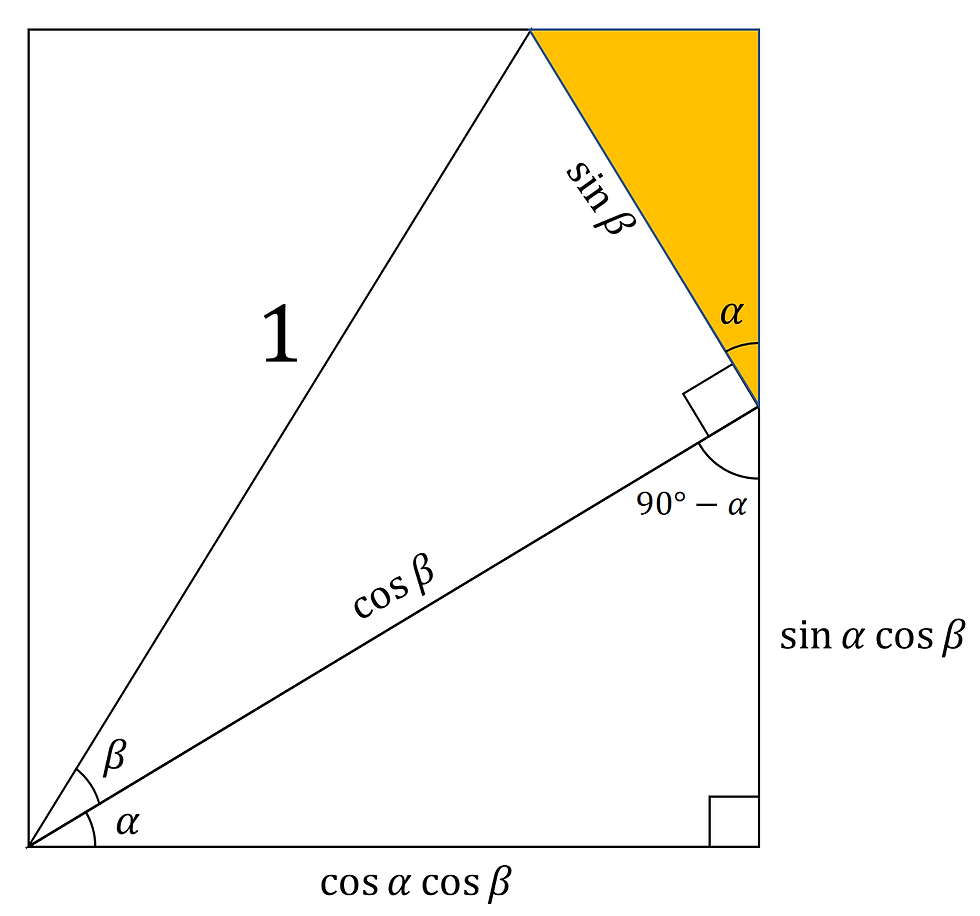
So in fact, this triangle is actually similar to the main triangle with α.

We can then proceed to label its lengths:

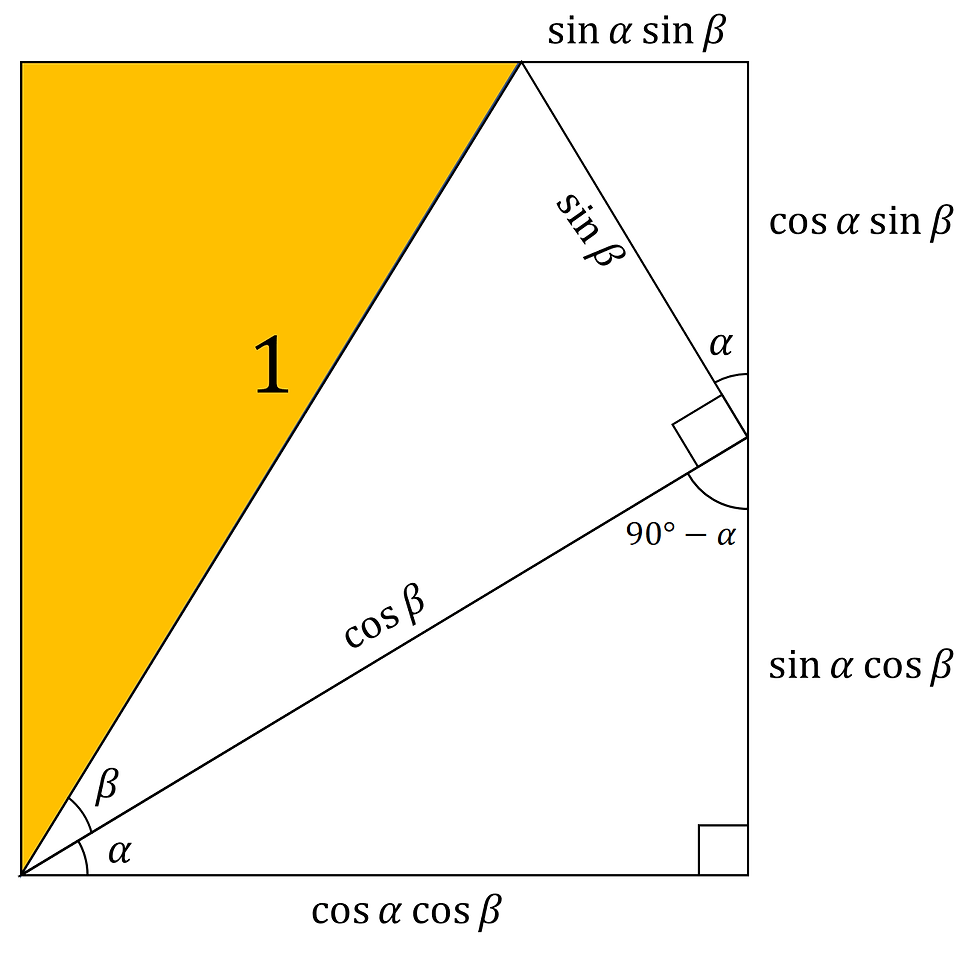
And now, focusing on the last unlabelled triangle, shown here in orange, we notice that we can apply alternate angles and label it like this:

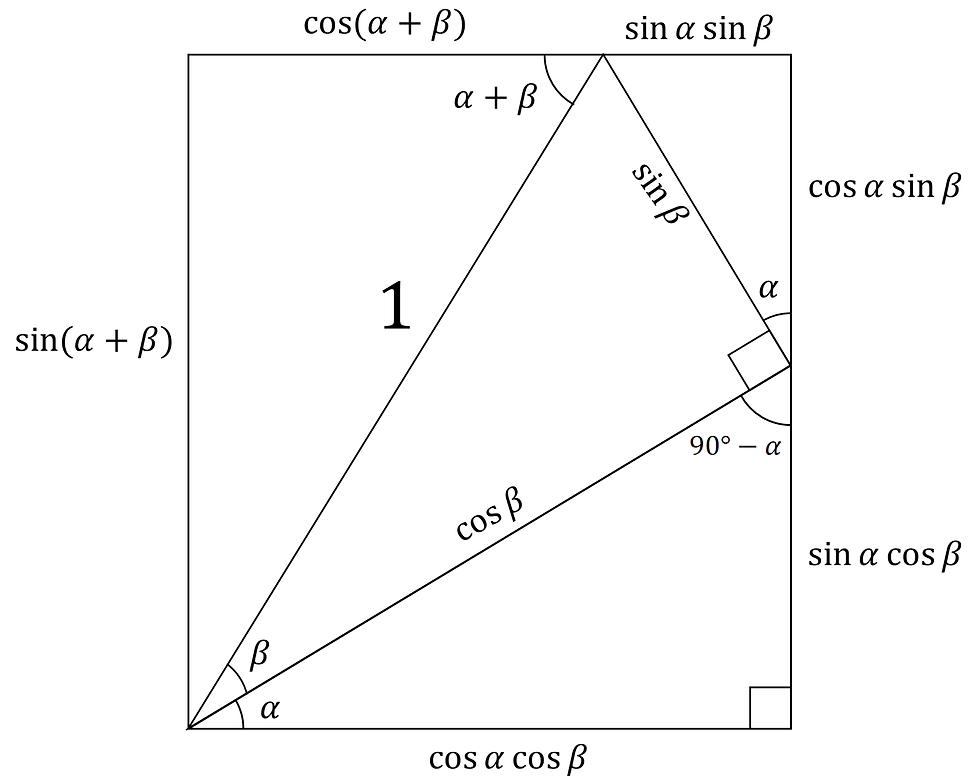
And with that, we are done.

Essentially what can be extracted out from this diagram is the formulae for the ratios of the sum of two acute angles.

Looking at the vertical edges of the bounding rectangle, all the terms must be equal to each other since they have the same length. Likewise for the horizontal edges.

Hence we can conclude these from the diagram:

This is called the addition formula / sum formula.

What about the difference formula?

Well, we can simply substitute β with -β and see how that works out. But before that, let's take a look at the phenomenon called symmetry.

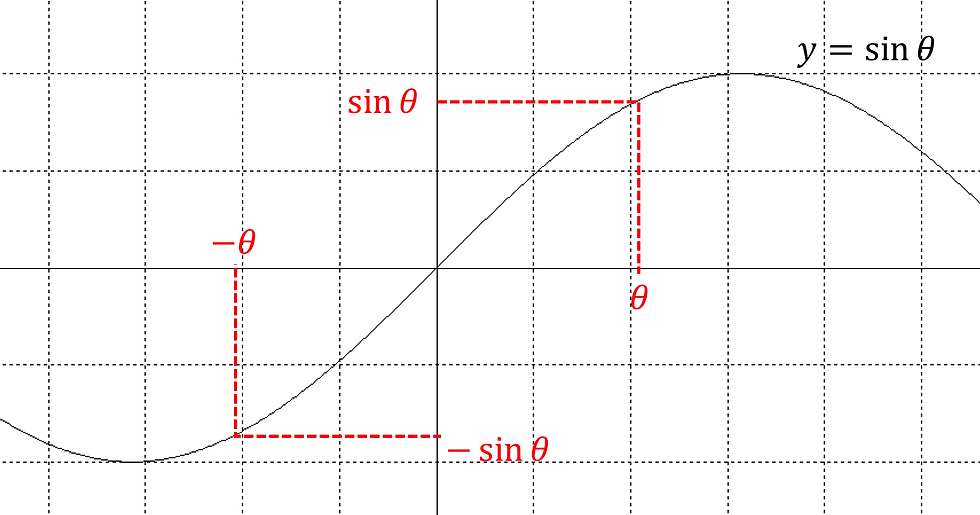
Plotting a sine graph, we can see that this is true:

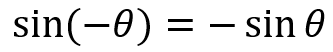
The symmetry is due to the periodic nature of the sine graph.

Likewise, we can do this for cosine too:

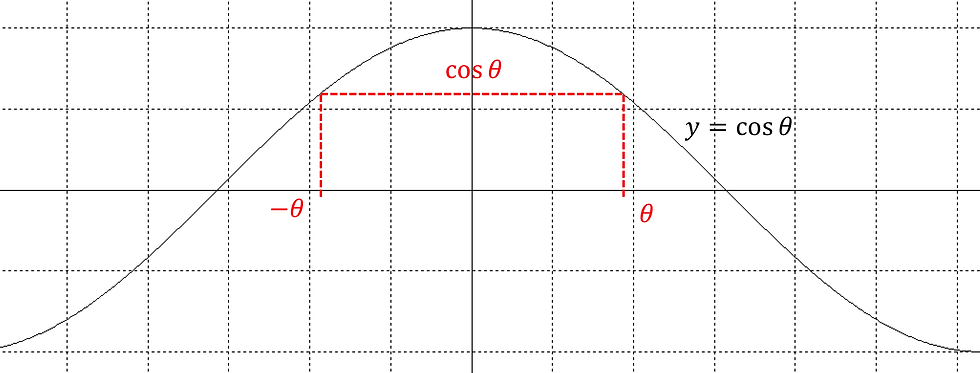
Now, we realise that this is true:

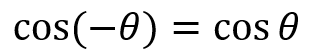
So for cosine, adding a negative to the angle doesn't change the outcome at all.

This is due to the fact that cosine is an even function, symmetric about the y-axis.

With these pieces of information, we can perform the substitution of β with -β and obtain the difference formulae.

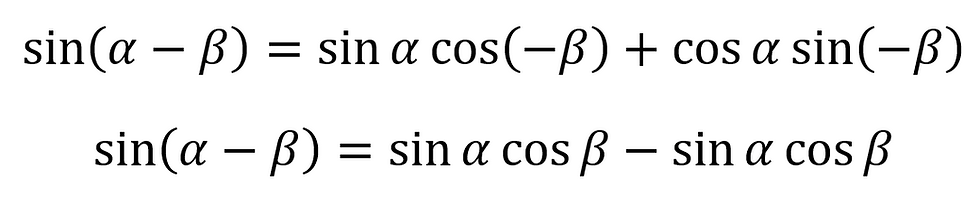
And for cosine:

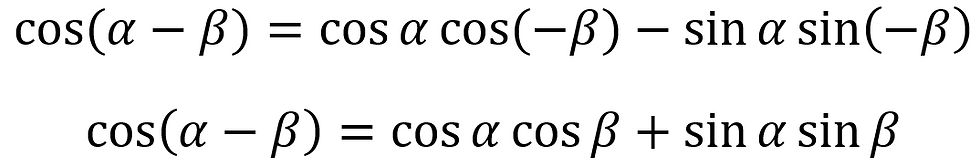
So now we have four identities, which can be condensed and written like this:

To get the identity for tangent, we can simply apply the knowledge from DT1 and take the quotient of sine and cosine:

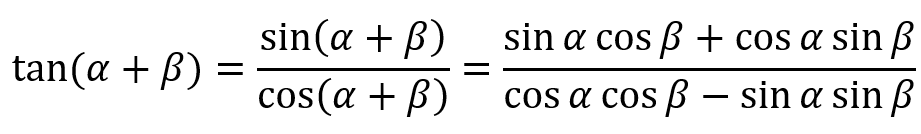
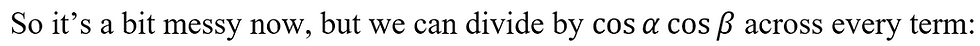
And to get the difference formula for tangent, we also substitute β for -β and simply, noting that tangent has the same symmetry properties as sine.

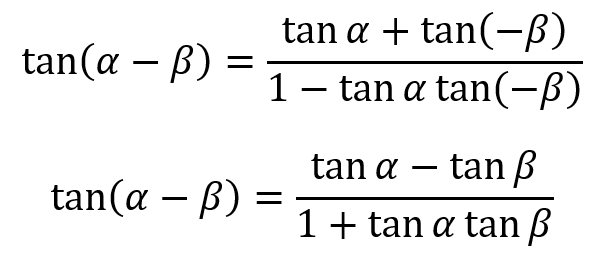
Then we can condense both tangent identities into one:

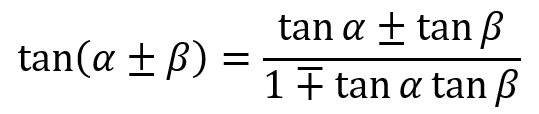
Here's a summary of all the identities we've derived (from scratch!) in this segment:

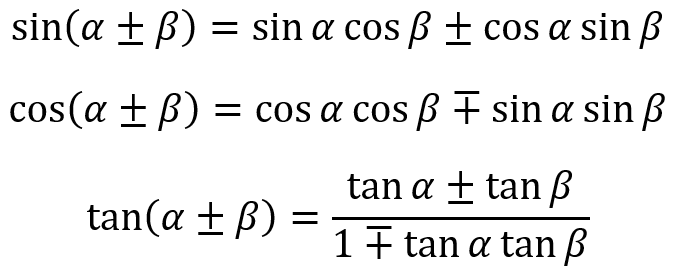
Next week, we will do more similar derivation.

Until then, thank you for reading! Stay tuned for more Messy Workings! :)