Logic Gates
- Jul 9, 2016
- 3 min read
Even though this information is available elsewhere on the internet, I feel like this site wouldn't be complete without it, so here's my breakdown of logic gates.
A logic gate is a device that takes in some number (a single or multiple) inputs and outputs a value. It is worth noting that these values of input and outputs are Boolean, meaning they are binary, either 1 or 0, true or false, yes or no, etc.
The first thing to learn is the name of the gates.

Let's start with the simplest gate, called the NOT Gate. It's also known as the Inverter because that's what it does.
An inverter takes a input signal and inverts it, providing the opposite signal as the output.
This table showing all possible inputs is called a truth table. This is the NOT gate's truth table:

The NOT gate's truth table is simple because there's only a single value as the input.
For multi-valued inputs, the number of combinations is two raised to the number of inputs.
Let's take a look at the AND gate.

The AND gate takes two inputs and only output a positive signal when both signals are positive.
Every gate has its inverse, which is equivalent to adding an inverter at the end of it. In the case of the AND gate, the inverse is called the NAND gate:

Basically the NAND gate only gives a negative output when both inputs are positive. It's basically inverting the output of the AND gate.
Another type of gate is called the OR gate:

The OR gate gives a positive output as long as either one of the inputs is positive.
Then there's also its inverse, the NOR gate:

The NOR gate gives a positive output only when both the inputs are negative.
Here's where things get a little more interesting. The XOR and XNOR gates function differently from the gates previously mentioned.

This is the XOR gate. It gives a positive output only when both inputs are different.

The XNOR gate gives a positive output only when both inputs are the same state.
These logic gates can be wired together in fancy ways to make a logic circuit, an example is this full adder shown below.

The truth table of the full adder is shown below, it is so named because the full adder is used to add two numbers together.

The S output means Sum, and the Cs mean Carry.
Because of the 'strictness' of the AND gate, it is treated like multiplication, and written as a dot in linear form.

The OR gate can then be treated like addition, bearing in mind that 1+1 isn't actually 1.

Therefore, any complicated logic circuit can be written in linear form. For example, consider the following circuit:

Letting the inputs be A and B, and letting the output be C, this circuit can be written as such:
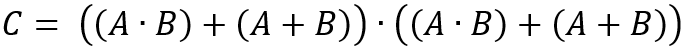
Sidenote: This is essentially an OR gate, if you trace the circuit.
The NOT gates (or any negation) can be written as a bar over the letter(s).
Let's modify our previous circuit to include some negations.

I selected random gates to switch out for their negated versions. This created a circuit with a positive output, independent of the input. Regardless, this (useless) circuit can be expressed as such:

De Morgan's Law states that:

Let's build circuits to compare.

Using this, we can see that these two circuits are essentially equivalent. De Morgan's law also shows up in Set Theory, and can be expressed in English as such:
1. The negation of a conjunction is the disjunction of the negations.
2. The negation of a disjunction is the conjunction of the negations.
We can hence check theoretically if our circuit is the most economic design before building it. These two circuits are the same, but one uses 3 gates, while the other uses 2.
Also, the theory helps to provide alternatives should we run out of one type of gate, for example.
There is much more to be explored about logic gates and Boolean logic. This has been a brief beginner's guide for logic gates and truth tables. Thank you for reading :)
==EndNote==
Try building your own logic circuits here now!














Comments