DT2 | Deriving Trigonometry - The Unit Circle

This segment will focus on building the intuition of expressing functions in terms of lengths around the unit circle.

A unit circle has a radius of 1 unit.

Suppose we have a unit circle with the angle θ subtended:

This would form a triangle OPQ with the radius as its hypotenuse:

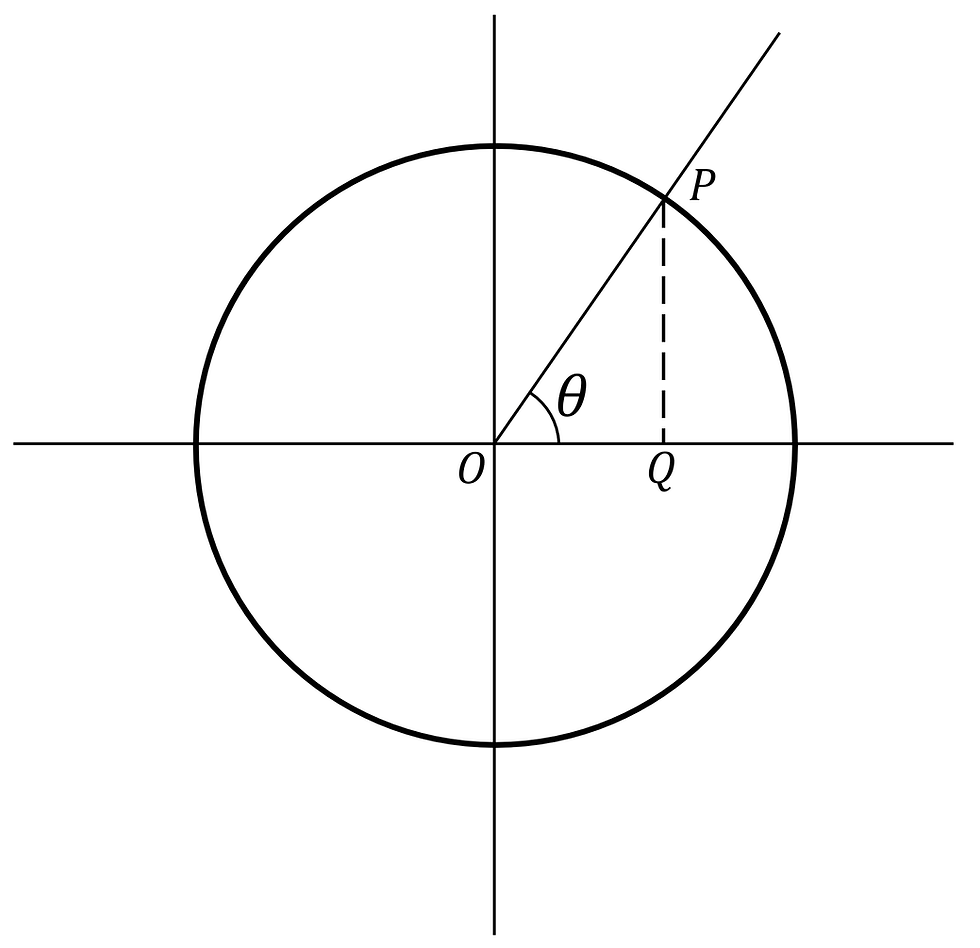
Since the hypotenuse is of length 1 unit, the lengths of the other sides of the triangle can be labelled as such:

This makes sense because:

By extension, the tangent function can also be defined:

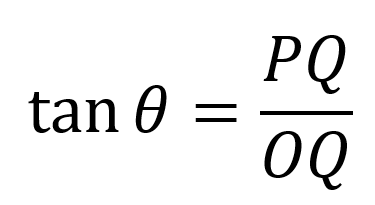
Hence on the diagram, the tangent function is the length shown here:

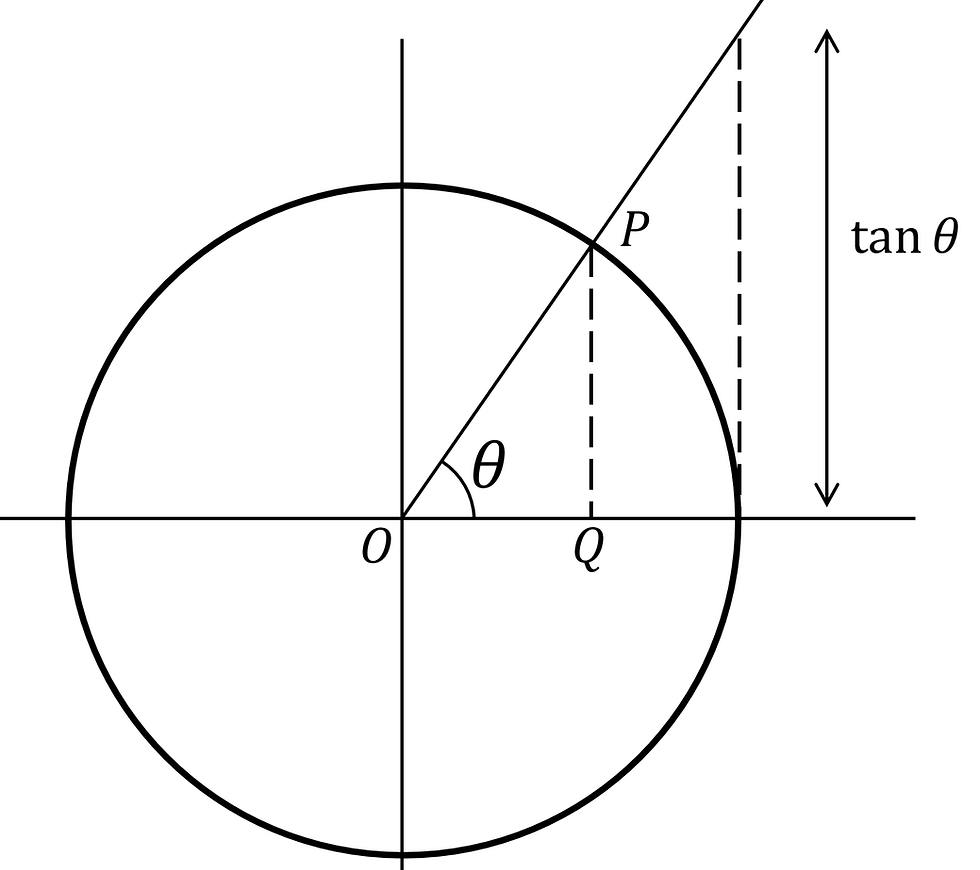
Knowing how, or at least having the intuition to express trigonometric functions as lengths around the unit circle is important because we will use many geometric proofs later on when deriving other identities.

Stay tuned for more Deriving Trigonometry!