Deriving Trigonometry: A Series

Recently, I looked back on how I learnt trigonometry and how schools taught it, and I realised that I've been trigonometry wrongly.

I was taught, perhaps comparable to other topics in mathematics, that there is a certain way to tackle trigonometry-related problems. There are rules, and we have to remember them by heart before anything makes sense. Trigonometry in my memory was a mess of formulas and identites that all needed to be memorised or referred to in lengthy formula sheets, and there was no other way around it.

Turns out, after taking a break from it for a while and then re-learning it again few years later, I can learn things that are so drastically new to me that are really worth sharing.

This 7-part series aims to cover the derivation (from scratch) of all the formula we were made to memorise or refer to the formula sheet without further elaboration on how they make sense.

The first of these is a simple one. It is often said that there are 3 common trigonometric functions, namely the sine, cosine, and tangent functions.

The usage and representation of each function is shown in the following table:

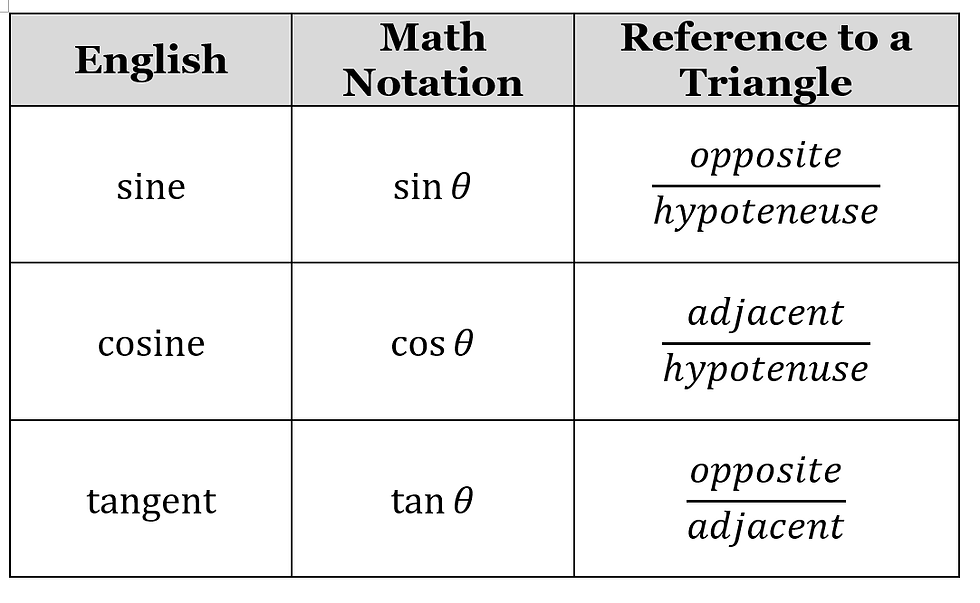
This is usually first shown to students with the accompanying diagram of a triangle being labelled as such:

The first pre-requisite to Deriving Trigonometry is this:

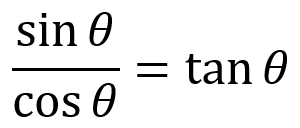
Looking at this with reference to the right triangle, we see that it makes sense:

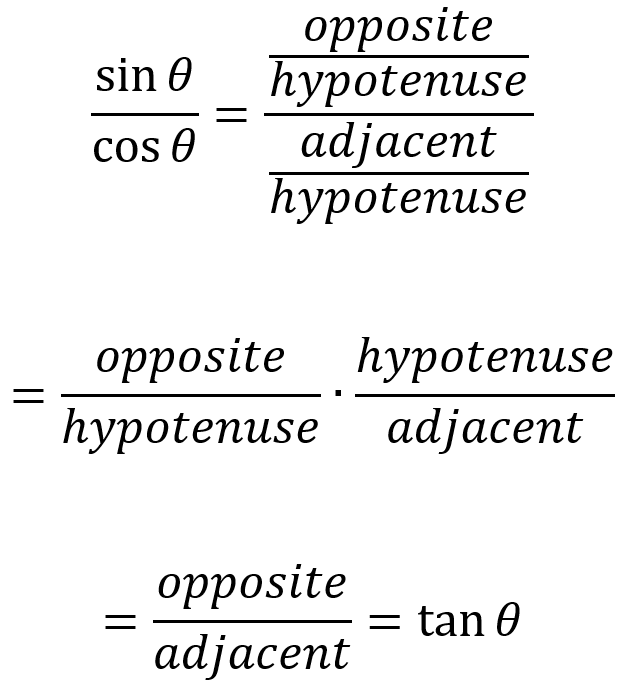
This turns out to be a very important identity, because now we only need to know the identities for sine and cosine, then we could divide it up to get the tangent identity.

This is why I put it as the first pre-requisite to this 7-part series.

Deriving Trigonometry will be continued next week. Thanks for reading!