General Form for Nested Radicals

It seems like as mathematicians, we like to find general forms to make our lives easier.

Last week's example on nested radicals could really be expressed as a specific case of a general form:

As such, we could start with the expression on the right, and end up with an expression without nested roots:

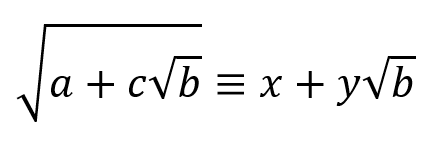
So to solve for x and y, we can approach it with the same technique as we did in the previous article, by squaring both sides and then equating the coefficients of the surds and the rational parts.

This would look like this:

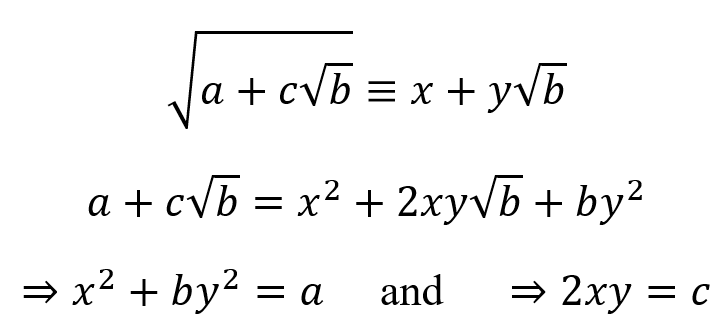
We can then apply a whole bunch of algebra into simplifying this system of simultaneous equations, keeping in mind that our end result should not contain x or y.

Upon obtaining what is actually a quadratic expression, it is worth noting that if a, b and c were fixed numbers instead of variables, this expression can be factorised by other means, like the cross method. However, dealing with variables means that we can only factorise this by the quadratic formula, or completing the square.

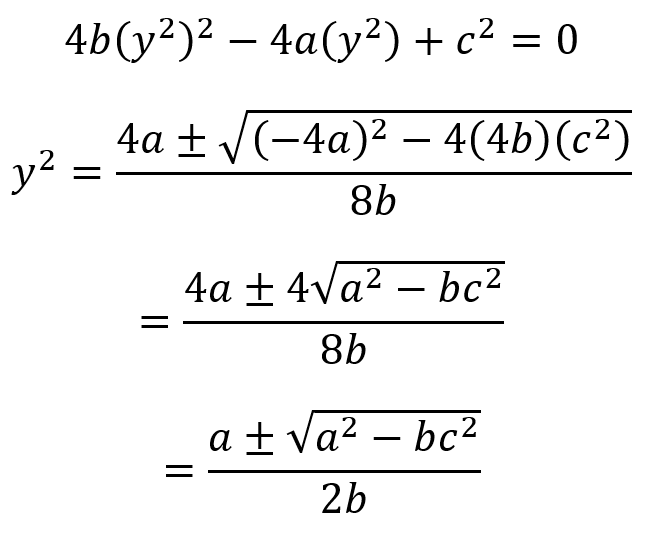
This means that y is as follows:

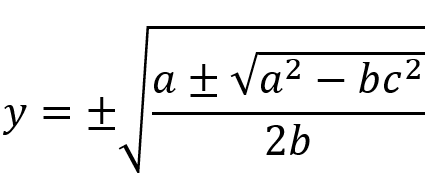
In an ironic sense, the solution to a nested radical is a nested radical.

However, the contents of this nested radical are made up of known constants, a, b and c.

We can then solve for x:

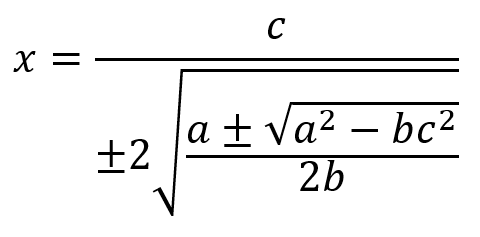
As such, we get our final equation:

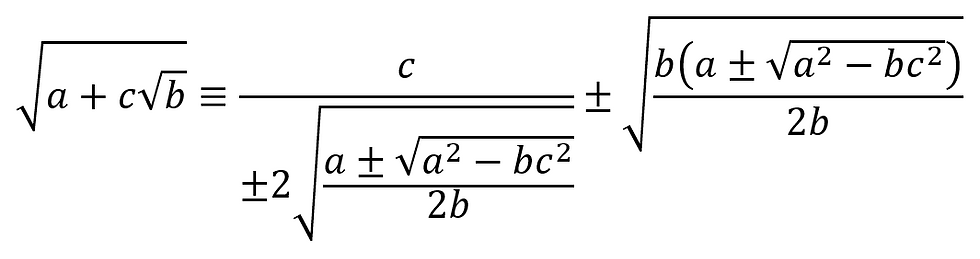
Because of the plethora of plus-minus signs, we will get 16 answers from this simplification. Bear in mind that many of them would be duplicates, and we would also need to reject any complex answers we get.

We will then be left with the two correct answers.

Thanks for reading!