Nested Radicals (Simple Example)

So it's been a while since we did some algebra.

If you've stumbled upon the concept of Nested Radicals before (which is what I can only describe as a very unfortunate event), then you know that this concept reaches far deeper than what this post will provide.

This post aims to provide a very brief introduction of the concept.

Consider the following:

Although not easily evaluated, one may intuitively wonder if this can be expressed in the following form:

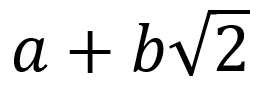
where a and b are both rational numbers.

This is an un-nested, linear form, and is much neater to work with.

We can test this by forming the equation like this:

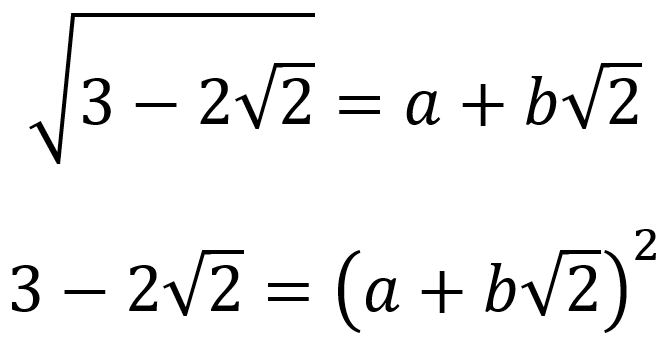
Should we fail to solve for a and b, then we can safely say that our intuition earlier was incorrect.

Working from here:

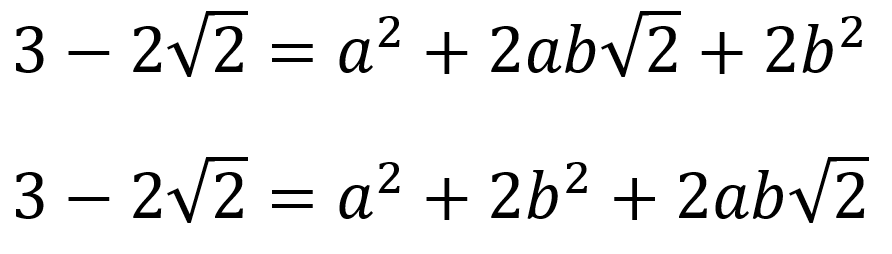
We can then compare the coefficients of the two distinct parts, almost treating this as a complex number.

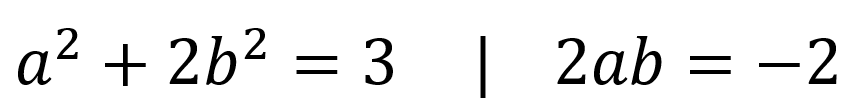
Looking at the equation on the right, we can get this:

We can then substitute this result to the equation on the left, to obtain this:

Taking a look at the result on the left:

Since we already established that a and b are rational, this result must be rejected.

The other result:

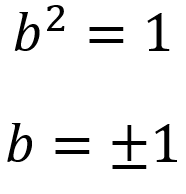
Substituting this result back into the equations to solve for a:

Hence we have our answers:

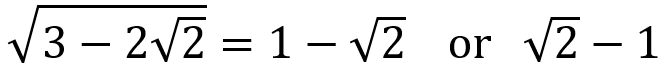
To check, we can simply square our two answers.

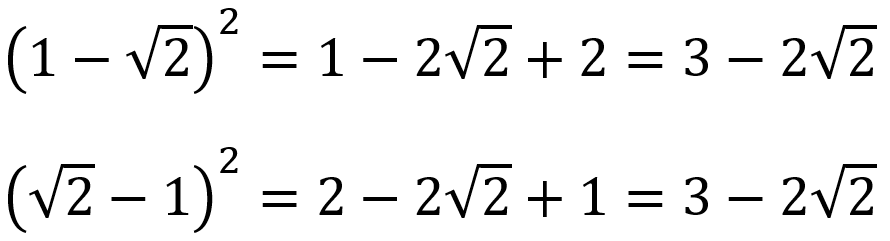
Hence, our answers are correct.

Thanks for reading!