Magic Trigonometry Hexagon
- YouWei
- Jul 16, 2016
- 2 min read
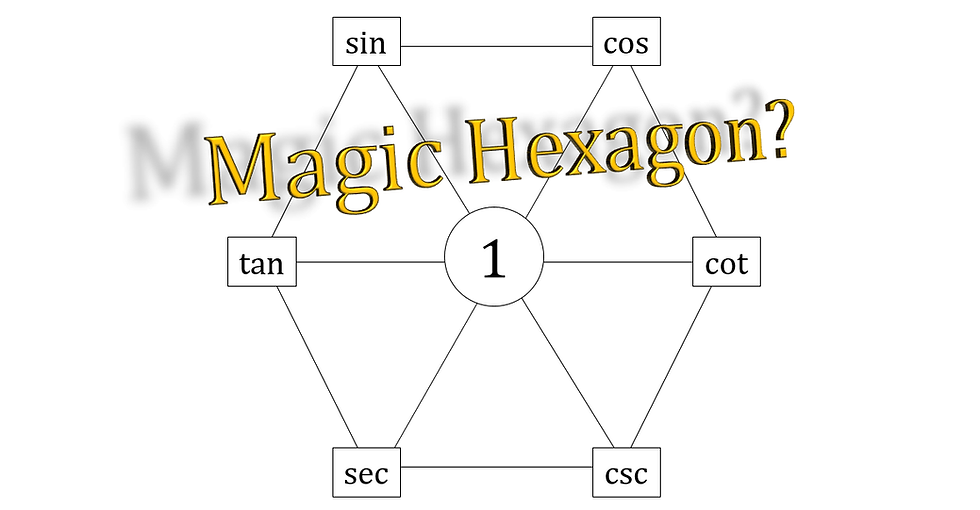
I want to share a neat trick to remembering some trigonometric identities. I first learnt that this is called the Johnson Diagram, but after searching for it online and learning that there's no actual name for it, I stopped giving credit to this Johnson guy and stopped calling it that.
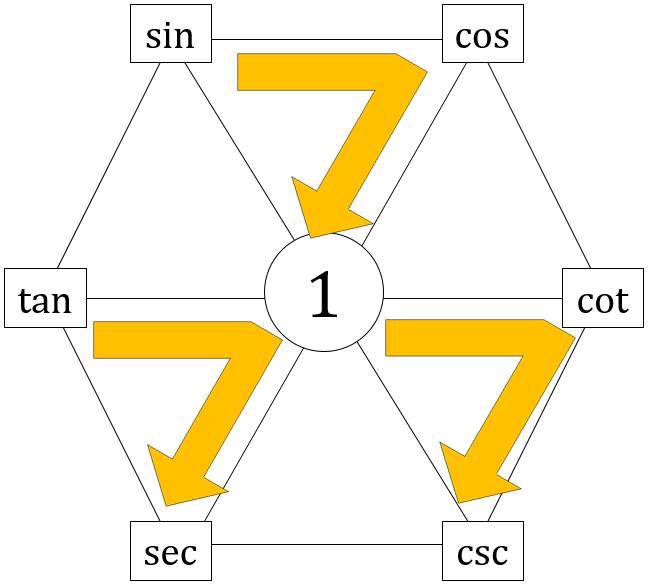
Here's the diagram:
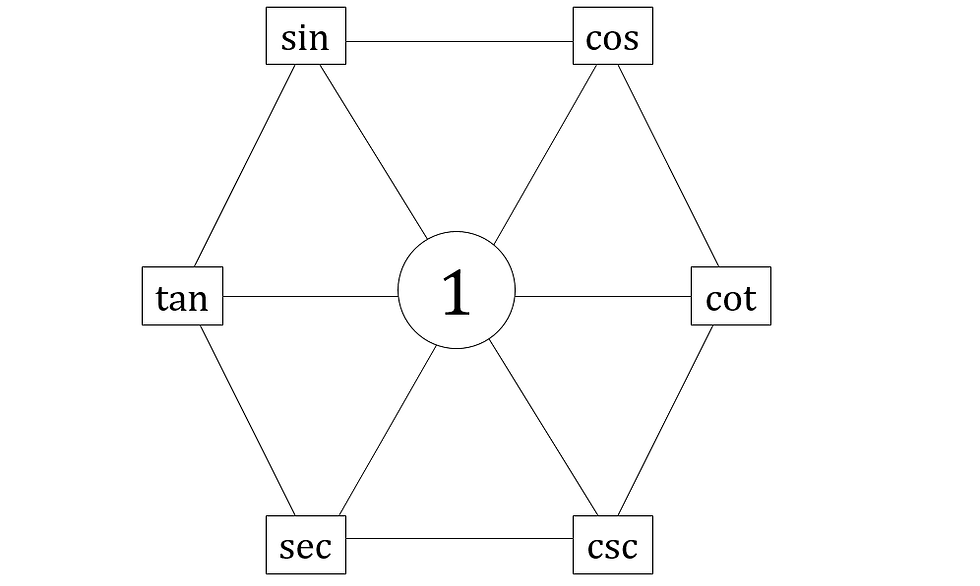
There are several ways to read it:
1. Quotient Rules
- Any 3 adjacent elements, going clockwise around the perimeter
- Any 3 adjacent elements, going anticlockwise around the perimeter
2. Product Rules
- Any 3 elements on the perimeter, converging from the outer pair to the central one
- Any 2 elements opposite to each other, converging to 1.
3. Reciprocal Rules
- From any perimeter element through the diameter to the opposite element
4. Equivalence Rules (or Complementary Angles)
- Any element on the left to the corresponding element on the right
5. Pythagorean Rules
- Going clockwise around any downward pointing triangle, starting from the top left point.
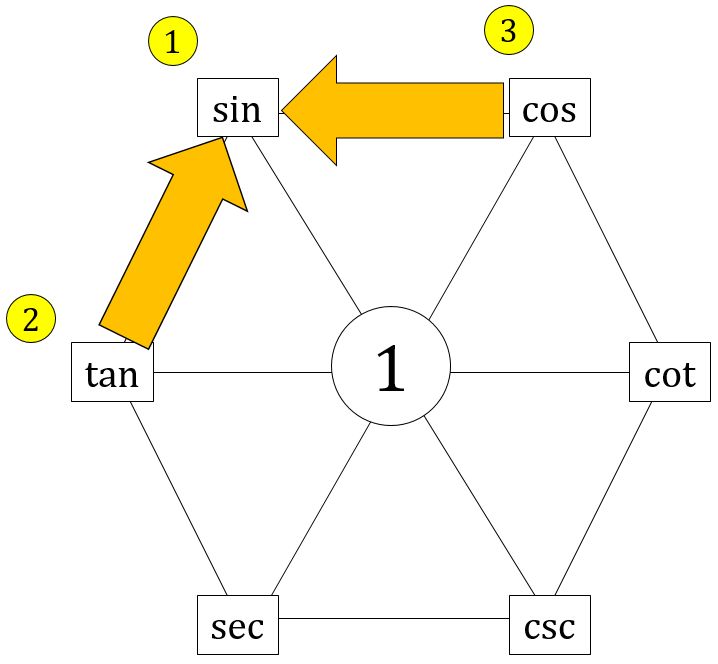
1. Quotient Rules
- Any 3 adjacent elements, going clockwise around the perimeter
- Any 3 adjacent elements, going anticlockwise around the perimeter
The quotient rules are read like this:

This will create 6 identities going clockwise and 6 more going the other way.

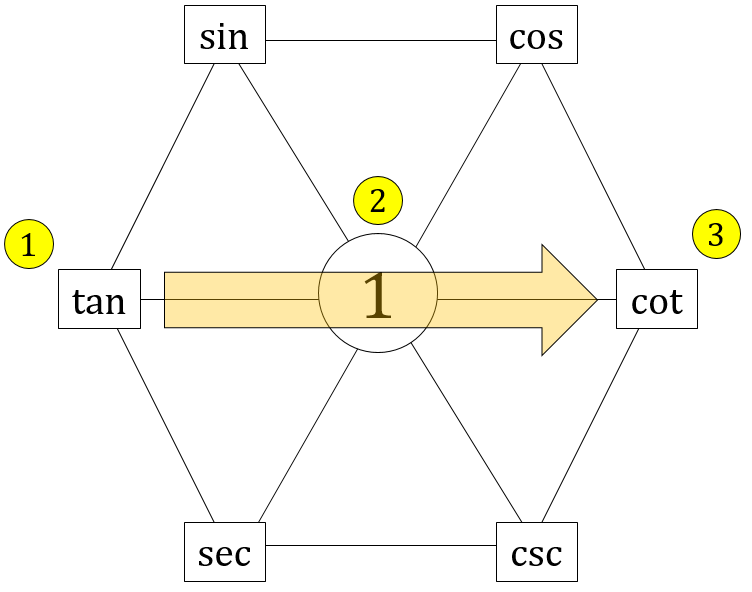
2. Product Rules
- Any 3 elements on the perimeter, converging from the outer pair to the central one
- Any 2 elements opposite to each other, converging to 1.
There are two very different ways to read the product rules.
This will yield to the following identities:

We could also read it like this:

Reading like this gives 3 identities:

These are essentially the same identities as the following reciprocal identities:
3. Reciprocal Rules
- From any perimeter element through the diameter to the opposite element
Instead of converging to the central 1 (implying multiplication), start from one side and end at the opposite side.
This will yield 6 identities:
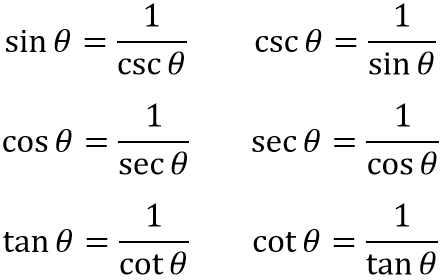
4. Equivalence Rules (or Complementary Angles)
- Any element on the left to the corresponding element on the right
The equivalence rules are read like this:

This gives us 3 identities:
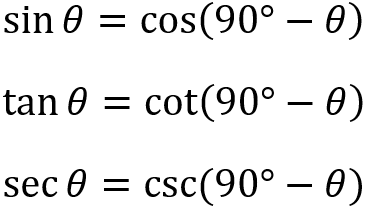
5. Pythagorean Rules
- Going clockwise around any downward pointing triangle, starting from the top left point.
The last one is pretty special and is read like this:
This will give us the 3 Pythagorean identities:
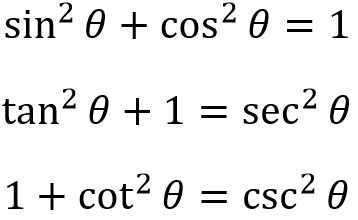
So these are the 33 formulae in this Magic Trigonometry Hexagon. Thanks for reading~














Comments