Harmonic Series is Divergent
This is a short post.
The harmonic series, so named because of its relation with musical overtones, is this:
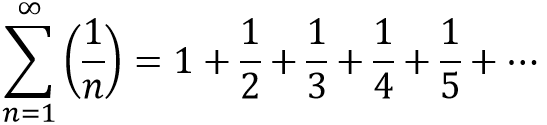
At first glance, it may be quite hard to see if it diverges or converges. The ratio between terms is not constant, meaning this series is not a geometric progression.
However there is a simple way to prove that this series is in fact, divergent.
Consider this series:
Ignoring the first term, this series is clearly divergent. The ratio between each term is 0. Continuously adding up the same number is not going to approach a fixed value.
We could split this series into this:
And compare this to the harmonic series:
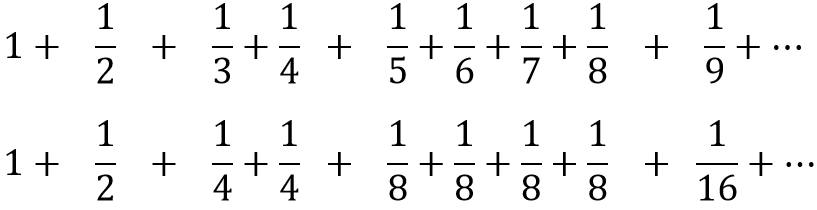
It is clear that the harmonic series (above) is greater than the divergent one. This means that the harmonic series also has to diverge.
This proof, first proposed by Nicole Oresme, is one of the many ways to prove the divergence of the harmonic series.
