Maximum Area of A Trapezium
This is a short post.
While writing the previous post about the trapezoidal Koch curve, there was a part of me that wanted to make the trapezium more general, like the angle of inclination. 60° was chosen because it was similar to the regular Koch, but the angle can be anything.
It's also interesting that 60° gives the maximum area of a trapezium, given that the slant height and short length are equal.
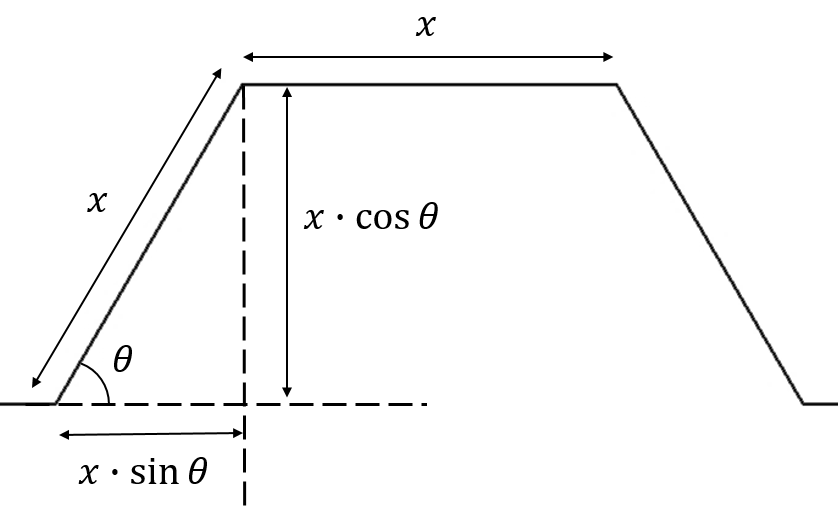
And here's the graph, where we take the length of x as 1.
Notice the point of maxima, in red, at π/3. Also notice the point in purple, at θ = π/2, where the height is perpendicular to the base, forming a square. The area is 1 at this point.
