Area of the Koch Curve

This is the Koch Curve. It is a fractal curve, this means that it has the same properties at every scale, no matter how much we zoom in / out.

Zooming in on the Koch curve looks like this:

Because there are infinite iterations, it can always be zoomed in upon, much like the points on a line.

It's easy to construct a Koch Curve.

We start with a straight line with an equilateral triangle on it.

This is the first iteration.

There are a few ways to get to the next iteration.

We could look at it in this way: Trisect each line and add an equilateral triangle in the middle section of each line.

Or we could scale down the entire iteration and plant that on each line made by that iteration, replacing each line with a line with a triangle.

Either way we get the next iteration:

We keep repeating this several times.

Once iterated forever, we have the Koch Curve.

There are two properties of this peculiar shape that one may wish to examine immediately. These are the area and perimeter of the curve.

We know the area is increasing because each iteration adds more triangles. However even after infinite iterations, the curve doesn't seem to extend beyond a certain bound. There appears to be a limit to the area.

Let's find that out.

We first need to work out an expression for the area of an equilateral triangle. There are many ways to do this.

I did this:

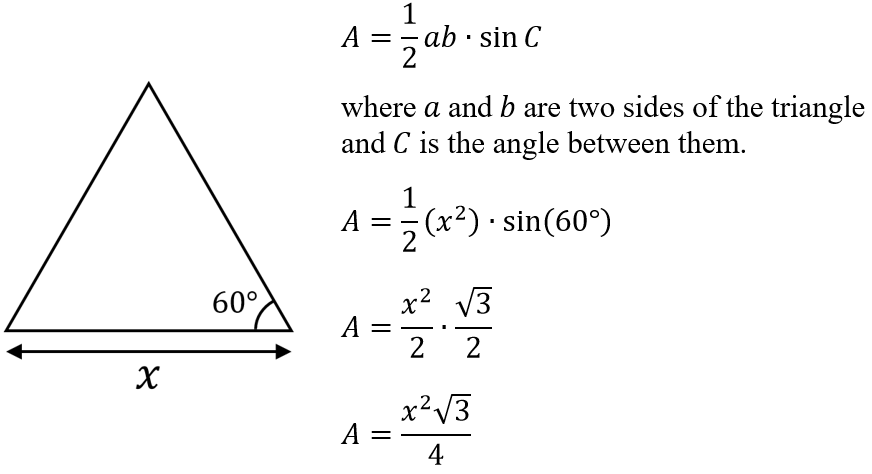
Now let's establish that the length of the initial straight line is 1.

This means that the area under the first iteration is as follows:

The next iteration adds 4 smaller triangles, and the area can be found like this:

Also, since we're eventually going to come up with an expression for the infinite iterations, the expression shouldn't be simplified just yet. It can all be done later.

Each iteration 4 times more triangles, and each time, the triangles are one third as the size of the previous iteration's. So the next iteration is easy to work out:

In fact, the area of the k-th of the curve would be this:

And hence by replacing k with infinity, we can find the limit to which the area converges to (if it does).

And we see that the summation part is a geometric progression:

The area of the final Koch curve is hence this:

This is surprising, because it is a constant value. It is fixed and invariable. If we start with a straight line of length 1, and iterate forever, to a shape we can't even define properly, we can define the amount of area it covers.

In fact, we can go an extra step and draw a bounding triangle around the Koch curve that the area never exceeds.