Constructing Square Roots
- YouWei
- May 14, 2016
- 2 min read

Geometrical construction only allows for two tools - a straightedge and a compass. A straightedge is like a ruler. It has infinite length, and no markings. We can only draw straight lines with it.
With a compass and straightedge, we can do some cool things.
We can double the length of a given line just by using the compass.

First, open up the compass to the length of the line.
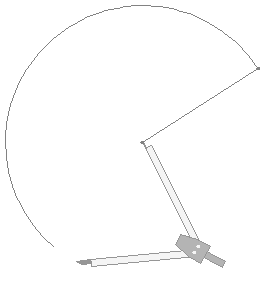
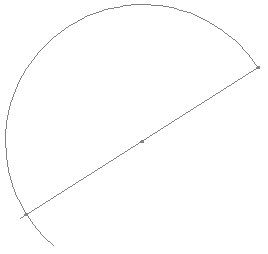
Draw an arc, more than a semicircle, using the length of the line as the radius.
Extend the line until the further end of the arc.
There, we have doubled the length of the line.
Bisecting a line isn't hard either.
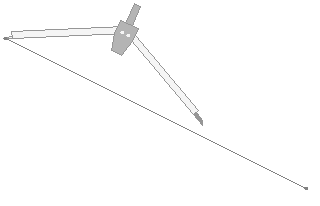
Open up the compass to more than half of the line segment.

Make an arc.

While maintaining the compass, draw another arc from the other end of the line segment.

Connect the points where the arcs intersect.
A question posed was whether it was possible to construct the square root of a line segment. Turns out, we'll need a marked ruler for that.
We first extend the line by 1 unit.
Here, there are 3 points on the line. The larger segment is the original line, and the shorter segment is the extension, of length 1 unit.
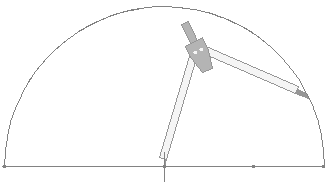
With this new line, we use it as the diameter and draw a semicircle.
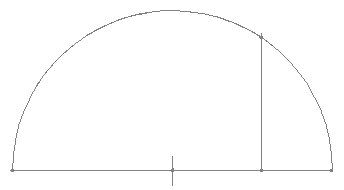
Then we draw a perpendicular line up to the semicircle. This line is exactly the square root of the original line.
This got me thinking, how can we prove this?
We can let the length of the original line be x, then the extension would make the diameter x+1.
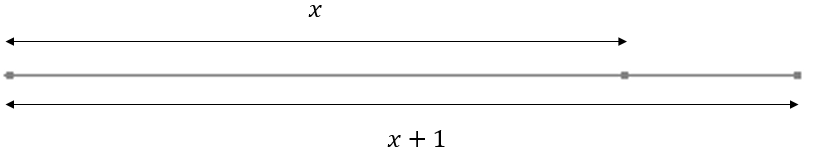
Then this would be the radius of the semicircle.
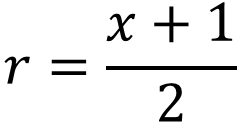
Since the hypotenuse of the triangle is also the radius, we can now label all the dimensions as such:

If we want to find out the length of the unknown side labelled with a question mark, we can use the Pythagoras' theorem, since it is a right angled triangle.
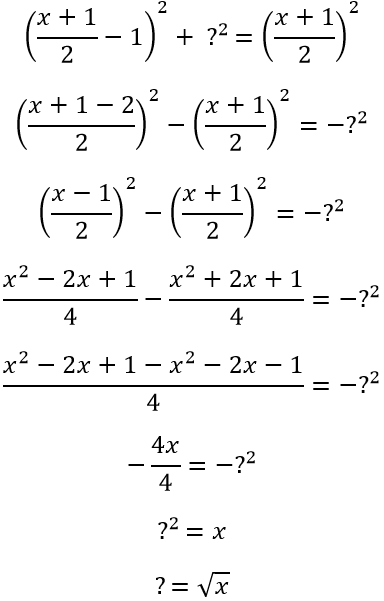
And there, we've proved it :)














Comments